Hello and welcome to Midas technical clinic.
This issue is a long story.
Let’s get to the point.

The rectangular section in the figure below is known as B = 400mm, H = 500mm, as = as’ = 40mm, as = as’ = 1962.5mm2, FC = 13.8mpa, FY = FY ‘= 330mpa, axial force nd = 600kN and bending moment MD = 50kN m.
Check the bearing capacity.
(the eccentricity increasing coefficient is not considered) the following is the manual calculation process of asking the Engineer: assuming that it is large eccentricity and the compression reinforcement yields, since FYAs = fy’as’, there is: nd = fcbx, and the data brought in is x = 108.7mm, X< ξ Bh0 = 0.56 * 460 = 257.6mm and x > 2As = 80mm, large eccentricity and yield of compression reinforcement, the assumption is true.
According to the moment balance of section centroid: Mn = FYAs (H0 as’) + fcbx (H / 2-x / 2) = 389.40kn m> MD bearing capacity meets the requirements.
The above calculation process seems to have no problem, but modeling in civil, importing CDN checking calculation, checking the detailed calculation sheet, it is found that although the checking calculation results are that the bearing capacity meets the requirements, the height of the compression area calculated by CDN is actually different from that calculated by hand, and even becomes a small eccentricity in CDN! Carefully observe the calculation process of CDN, or assume large eccentric compression first, but the balance equation listed in the calculation of the height of the compression area is the moment balance of the action point of Nd, resulting in the calculated height of the compression area is different from the above manual calculation, which seems to be no problem.
It seems that there is no problem through the manual calculation of the balance equation of the force on the section.
Why is the large eccentricity obtained by one algorithm for the same member, The other is small eccentricity? Which method is wrong? Let’s start with the conclusion: both methods are OK.
Carefully analyze the above two methods.
The first manual calculation method actually takes the axial force nd as a known quantity to solve the maximum bending moment that the section can bear under the action of axial force nd is Mn = 389.40kn m.
Greater than the design bending moment MD = 50kN m.
It is determined that the bearing capacity meets the requirements, that is, the actual solution is n = 600kN and M = 389.40kn The height of the compression zone corresponding to the limit state of M is large eccentric compression; The calculation method of CDN is to take the eccentricity E0 = m / N as the known quantity.
The maximum axial force that the calculated section can bear is NN = 1840kn, which is greater than the design value of axial force.
It is determined that the bearing capacity meets the requirements, that is, CDN solves n = 1840kn, M = 1840 * (50 / 600) = 153kn The height of the compression zone corresponding to the limit state of M is small eccentricity.
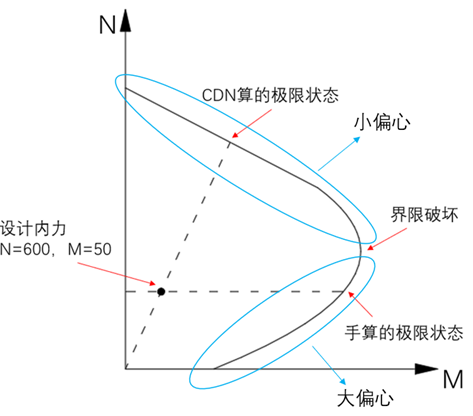
This problem can also be better understood in combination with the following P-M curve: finally, we can summarize that the height of the compression zone calculated according to the force balance on the section is actually the height of the compression zone when the member reaches the limit state of bearing capacity, rather than the height of the compression zone of the member in the design internal force state.
Under the design internal force state, because neither concrete nor reinforcement reaches the ultimate strength value, We cannot get the actual height of the compression zone according to the internal force balance of the section.
OK, that’s the end of this issue.
If you feel you have gained something, please help us pay attention.
Thank you for watching this article, which is a non rigorous technical course.
It is inevitable that there are omissions.
Please criticize and correct more! welcome.


